名词解释
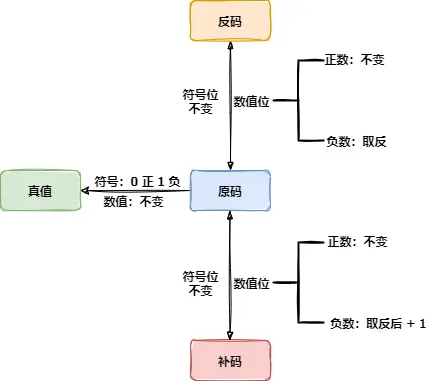
原码:原码是最简单的整数表示方法,其中最高位用来表示符号(0表示正数,1表示负数),其余位表示数值的绝对值。例如,+5的原码是00000101,-5的原码是10000101。
反码:反码是通过对原码取反得到的,即将正数的原码保持不变,负数的原码的所有位取反(包括符号位)。例如,+5的反码是00000101(与原码相同),-5的反码是11111010。
补码:补码是计算机中最常用的整数表示方法。正数的补码与其原码相同,而负数的补码是其反码加1。补码的特点是在进行加减法运算时,不需要单独处理符号位。例如,+5的补码是00000101,-5的补码是11111011。
移码:移码是一种不常见的整数表示方法,在计算机领域中较少使用。它与补码类似,但是所有的数值都被偏移了一个固定的值,通常是一个中间值,以使得正数的表示始终比负数的表示更大。这种表示方法在某些特殊的硬件设计中可能会使用。
例子
1.原码为正数
整数 +1
0000 0001 // 原码
0000 0001 // 反码 // 正数的 反码 = 原码
0000 0001 // 补码 // 正数的 补码 = 反码 = 原码
1000 0001 // 移码 // 移码 = 补码的符号位取反
2.原码为0
整数 +0
0000 0000 // 原码
0000 0000 // 反码 // 正数的 反码 = 原码
0000 0000 // 补码 // 正数的 补码 = 反码 = 原码
1000 0000 // 移码 // 移码 = 补码的符号位取反
整数 -0
1000 0000 // 原码
1111 1111 // 反码 // 负数的 反码 = 原码除符号位不变 其他全取反
0000 0000 // 补码 // 负数的 补码 = 反码+1 //这里由于越界,取后8位则结果为8个0
1000 0000 // 移码 // 移码 = 补码的符号位取反
3.原码为负数
整数 -1
1000 0001 // 原码
1111 1110 // 反码 // 负数的 反码 = 原码除符号位不变 其他全取反
1111 1111 // 补码 // 负数的 补码 = 反码+1
0110 1111 // 移码 // 移码 = 补码的符号位取反
应用场景
原码:符合人类直觉,是最简单的整数表示方法
反码:
1.诞生的前景:CPU擅长加法运算,因此为了提高运算速度,会将减法也转为加法 例如 1 - 1 会转为 1 + (-1) 。此时发现计算结果不符合预期
0000 0001 // 1
+ 1000 0001 // -1
——————————————
1000 0010 // -2
2.解决什么问题:解决原码运算中,将符号位也参与运算会导致计算结果不符合预期的问题。
0000 0001 // 1
+ 1111 1110 // -1
——————————————
1111 1111 // -0
0000 0001 // 1
+ 1111 1101 // -2
——————————————
1111 1110 // -1
3.还有什么问题:原码和反码都存在+0和-0的问题,计算-0会计算结果不符合预期的问题
0000 0001 // 1
+ 1111 1111 // -0
——————————————
0000 0000 // +0
补码:
- 诞生的前景:反码解决了大部分的计算问题,但是在连续计算中不可避免会出现-0导致计算结果不符合预期。
- 解决什么问题:原码和反码中 0的表示不一致,以及导致的运算错误的问题。(-+0)